问题
我们先来看这样一个问题:
给定数组A [2,3,51,32,56,1,1,3,….] 如何高效的查询 [start, end] 范围内的最小值 或者 最大值?
分析
暴力解法自然是遍历[start, end]范围内的数,取最小值;但如果查询非常频繁或者范围本身非常大,这个方法并不高效;
Sparse Table 就是解决这个问题的一种数据结构,其定义如下:
st[i][j] 表示下标为i的元素开始,长度为 2^j的子数组的和; 其中, i+2^j < len(A)
下图展示了sparse table计算过程中,如何利用前一轮的计算结果快速计算当前范围的极值
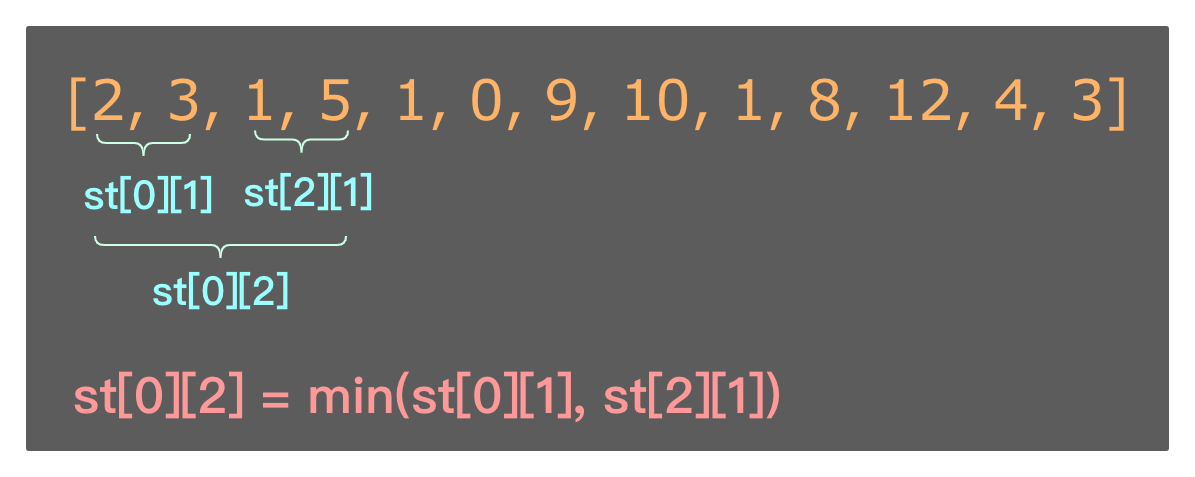
我们直接看代码
func main() {
nums := []int{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
spew.Dump(rangeMinQuery(nums, 4, 7))
}
func rangeMinQuery(nums []int, start int, end int) int {
max := int(math.Log2(float64(end - start + 1)))
st := buildSparseTable(nums)
// 注意这里的比较,start 和 end-max+1 之间是可能存在overlap的,但是这个对计算极值不影响
// 这也是为什么sparse table在这种场景下极为高效的原因
return min(st[start][max], st[end-max+1][max])
}
func buildSparseTable(nums []int) [][]int {
ans := [][]int{}
// 最大可能的幂次 即 2^maxpower <= len(nums)
maxpower := int(math.Log2(float64(len(nums))))
// 初始化
for i := 0; i < len(nums); i++ {
ans = append(ans, make([]int, maxpower+1))
}
for j := 1; j <= maxpower; j++ {
for i := 0; i+1<<j-1 < len(nums); i++ {
if j == 1 {
// 长度为2时,比较相邻元素即可
ans[i][j] = min(nums[i], nums[i+1])
} else {
// 长度为4, 8 ... 等时,利用上一轮计算的结果
ans[i][j] = min(ans[i][j-1], ans[i+1<<(j-1)-1][j-1])
}
}
}
return ans
}
func min(a int, b int) int {
if a < b {
return a
}
return b
}
注意
- 示例代码中,先进行sparse table的建立,然后进行查询,这只是为了方便展示; 实际问题中,一般需要预先建立sparse table,然后不断调用query去应对大量查询