题目描述
Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree, construct and return the binary tree.
Example 1:
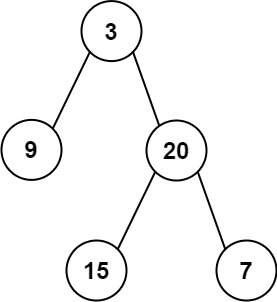
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]
Example 2:
Input: preorder = [-1], inorder = [-1]
Output: [-1]
Constraints:
- 1 <= preorder.length <= 3000
- inorder.length == preorder.length
- -3000 <= preorder[i], inorder[i] <= 3000
- preorder and inorder consist of unique values.
- Each value of inorder also appears in preorder.
- preorder is guaranteed to be the preorder traversal of the tree.
- inorder is guaranteed to be the inorder traversal of the tree.
题目分析
题目要求根据前序遍历和中序遍历的结果去构建一颗二叉树
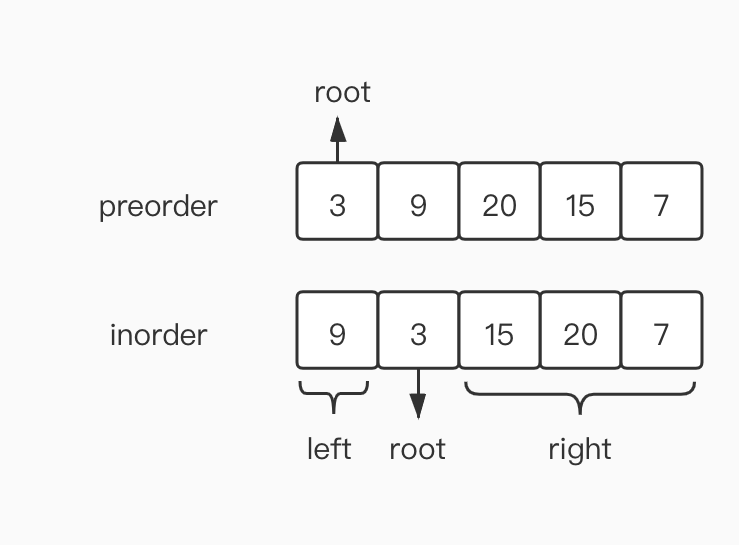
这里我们画一张图就能很直观的看到,对于preorder,第一个元素即为根节点;在inorder中,找到这个根节点的值后,它左侧即为左子树的全部节点,右侧为右子树的全部节点; 也就是说,左子树和右子树的中序遍历结果我们已经知道了,现在还剩下左右子树的前序遍历结果分别是什么未知。如果这个也能得到,我们就可以进行递归构建了
再次观察可知,对于一颗二叉树的中序遍历,如果左子树的节点数量为N, 则左子树加上根节点共有N+1个,而在前序遍历中,显然这也是成立的;既然前序遍历中的第一个为根节点,那么接下来的N个数即为前序遍历中左子树的结果;剩余数字为右子树的遍历结果
至此,我们可以计算出左右子树各自的前序、中序遍历结果,然后递归构建即可
代码如下:
示例代码
func buildTree(preorder []int, inorder []int) *TreeNode {
// 使用map记录中序遍历结果下各个节点的下标
inmap := make(map[int]int, len(inorder))
for k, v := range inorder {
inmap[v] = k
}
return build(preorder, inorder, inmap, 0, len(preorder)-1, 0, len(inorder)-1)
}
func build(preorder []int, inorder []int, inmap map[int]int, prestart int, preend int, instart int, inend int) *TreeNode {
if prestart > preend || instart > inend {
return nil
}
rootval := preorder[prestart]
root := &TreeNode{Val: rootval}
// left tree
root.Left = build(preorder, inorder, inmap, prestart+1, inmap[rootval]-instart+prestart, instart, inmap[rootval]-1)
// right tree
root.Right = build(preorder, inorder, inmap, inmap[rootval]-instart+prestart+1, preend, inmap[rootval]+1, inend)
return root
}