问题描述
There are n servers numbered from 0 to n-1 connected by undirected server-to-server connections forming a network where connections[i] = [a, b] represents a connection between servers a and b. Any server can reach any other server directly or indirectly through the network.
A critical connection is a connection that, if removed, will make some server unable to reach some other server.
Return all critical connections in the network in any order.
Example 1:
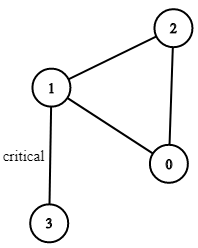
Input: n = 4, connections = [[0,1],[1,2],[2,0],[1,3] ]
Output: [[1,3] ]
Explanation: [[3,1] ] is also accepted.
Constraints:
- 1 <= n <= 10^5
- n-1 <= connections.length <= 10^5
- connections[i][0] != connections[i][1]
- There are no repeated connections.
问题分析
这道题触及到了知识盲区,没啥头绪。。。😭 查看题目提示, 要求使用Tarjan算法求解,一番搜索后关键信息如下:
要理解Tarjan算法,首先我们需要理解图论中的几个概念:
- 强连通 在有向图G中,如果两个顶点(vi, vj)有一条从vi到vj的路径,同时还有一条从vj到vi的路径,则称这两个顶点强连通
- 强连通分量 如果有向图G的任意2个顶点都强连通,则称G为一个强连通图;有向图的极大强连通子图,称为强连通分量
- 对于无向图, 极大连通子图 称为连通分量 (我理解无向图边是双向的,所以2点的路径不存在"强弱"关系,故"连通"即可); 概念和有向图类似,只不过由于是无向的,连通的点之间都满足两两连通条件;故一个连通的无向图的连通分量即为自身; 如果一个无向图由多个不相连的子图构成,这这些子图就是它的连通分量
- 桥 对于无向图,如果去除某条边后,该无向图的连通分量数量增加了,则该边称为桥。即去除该边后,原无向图的某个连通子图分裂成2个不连通的子图了
- 割点 对于无向图,如果去除某个顶点后,该无向图的连通分量数量增加了,则该顶点称为割点
而 Tarjan算法 就是用来求有向图的 强连通分量 的。而根据题意,我们需要求出无向图的所有桥; 我们先来看看对于有向图,如果要求强连通分量需要怎么处理:
Tarjan算法 定义了2个非常重要的数组:
- dfn[i] 表示对有向图进行dfs时的全局时间戳,也就是dfs时顶点的遍历顺序编号
- low[i] 表示从顶点i能够访问到的最小的 dfn; 算法采用回溯方式进行逐步更新
func tarjan(node int) {
// dfs遍历的全局时间戳, 标记顶点访问先后顺序
idx++
// 初始化当前顶点的 low[node] = idx
low[node] = idx
// 初始化当前顶点的 dfn[node] = idx, 这个值初始化后不会变化
dfn[node] = idx
// 栈中压入当前访问的顶点
stack.Push(node)
// 标记当前顶点在栈中
visited[idx] = true
// 遍历当前顶点连通的顶点
for _, v := range V[node] {
// 如果该子节点未访问过,执行dfs过程
if dfn[v] == 0 {
tarjan(v)
// dfs完毕后,需要将当前节点的low值更新为子节点的最小值
low[node] = min(low[node], low[v])
} else {
// 如果该子节点已经访问过,且已经在栈中, 说明该子节点实际上是当前顶点的“父亲”节点
if visited[v] {
// 此时需要将当前顶点的low值更新为该子节点的dfn最小值:
// 因为该子节点先于该顶点被访问,故需要更新当前顶点的low值为这类子节点的dfn值的最小值
low[node] = min(low[node], dfn[v])
}
}
}
// 如果当前顶点的low值与dfn值相等,说明:
// 该顶点是一个强连通分量的起始访问顶点, 即在dfs树中是某个强连通分量对应的子树的根;
// 如果不是根的话,该顶点的low值必定会被更新为一个更小的值,不会等于dfn[i]
if low[node] == dfn[node] {
// 从栈中弹出 node及之后的所有顶点,这些顶点构成一个连通分量
for {
top := stack.Pop()
// 记录连通分量
// mark()
if top == node {
break
}
}
}
}
那么回到无向图的桥这个问题上,从Tarjan算法我们知道,如果某个边属于某个连通分量,则显然即使去掉这条边,图仍然是连通的;那么一种方式就是求出所有连通分量后,判断所有的边是否属于连通分量;如果不属于,则为所求;
而如果这条边不属于某个连通分量,那么就有:
- 假设该边为 v1 —-> v2 (v1指向v2)
- 那么有 low[v2] > dfn[v1]; 即如果对于v2这个点,它能访问到的最小的顶点的序号是 大于 v1的,说明通过v2无法访问到序号小于v1的点,即非强连通; 那么该边即为所求
综上,代码如下:
示例代码
var (
low map[int]int
dfn map[int]int
idx int
)
func criticalConnections(n int, connections [][]int) [][]int {
ans := [][]int{}
m := make(map[int][]int)
// 遍历边,得到点的邻接点; 方便后续遍历
for _, v := range connections {
m[v[0]] = append(m[v[0]], v[1])
m[v[1]] = append(m[v[1]], v[0])
}
low = make(map[int]int, n)
dfn = make(map[int]int, n)
for i := 0; i < n; i++ {
if dfn[i] == 0 {
tarjan(0, -1, m, &ans)
}
}
return ans
}
func tarjan(node int, father int, m map[int][]int, ans *[][]int) {
idx++
// dfn[i]表示在整个dfs过程中,顶点i的遍历顺序(Tarjan算法中的时间戳)
dfn[node] = idx
// low[i]表示顶点i能够回溯到的最小的顶点时间戳; 初始化为自身的dfn[i],即初始只能回溯到自身
low[node] = idx
for _, v := range m[node] {
// 如果未访问过
if dfn[v] == 0 {
// 继续dfs搜索
tarjan(v, node, m, ans)
// 当前节点的low值更新为 所有子节点low值的最小值
low[node] = min(low[node], low[v])
// 判断桥: 如果当前节点相连通的子节点v的low值存在比当前节点更大的,说明该子节点v不存在一条路径,使得不经过 node--v 这条边 而连通到 小于等于dfn[node]的节点
// 换言之,如果 node--v 这条边被切断,v将无法连通到比dfn[node]更小的点(含node),即切断后,图不再连通; 因此 node--v即为所求的关键边的其中一条
if low[v] > dfn[node] {
*ans = append(*ans, []int{node, v})
}
} else {
// 由于是无向图,当前节点dfs时如果遍历的子节点非父节点,且已经访问过了,那么使用dfn[v]进行判断更新node的low值
if v != father {
low[node] = min(low[node], dfn[v])
}
}
}
}
func min(a int, b int) int {
if a < b {
return a
}
return b
}