问题描述
Given the root of a binary tree, return the length of the diameter of the tree.
The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.
The length of a path between two nodes is represented by the number of edges between them.
Example 1:
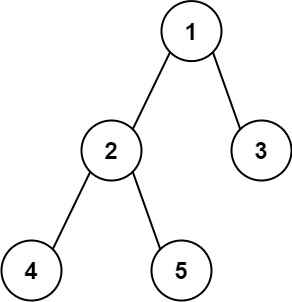
Input: root = [1,2,3,4,5]
Output: 3
Explanation: 3 is the length of the path [4,2,1,3] or [5,2,1,3].
Example 2:
Input: root = [1,2]
Output: 1
Constraints:
- The number of nodes in the tree is in the range [1, 104].
- -100 <= Node.val <= 100
问题分析
问题要求二叉树的直径,简单观察后可以发现,对于root而言,有2种形式:
- 直径所在的路径经过当前root,不难分析出,这种情况下,直径等于左树最大深度 + 右树最大深度
- 直径所在的路径不经过当前root,那么直径等于经过某个子树root的直径
那么将上述形式直接翻译为代码,即可得到初始解法
初始解法
func diameterOfBinaryTree(root *TreeNode) int {
if root == nil {
return 0
}
if root.Left == nil && root.Right == nil {
return 0
}
// case 1: 不经过root节点的,即 max(d(Left), d(Right))
res1 := max(diameterOfBinaryTree(root.Left), diameterOfBinaryTree(root.Right))
// case 2: 经过root节点的,即 path(距离Left最远的叶子节点,Left) + path(距离Right最远的叶子节点,Right)
res2 := getDepth(root.Left) + getDepth(root.Right)
return max(res1, res2)
}
func getDepth(root *TreeNode) int {
if root == nil {
return 0
}
return max(getDepth(root.Left), getDepth(root.Right)) + 1
}
func max(a int, b int) int {
if a >= b {
return a
}
return b
}
优化解法
初始解法提交AC后,查看评论区,发现有更简洁的解法;还是基于刚才的分析,进一步观察其实可以得出:
当前树的直径等于经过root的最长路径或者经过某个子树root的最长路径
那么我们可以对每一个节点都求出以该节点为root,且路径经过root的直径;在这些子树直径中,最大的那一个即为所求
因此我们可以得到一个更为简洁的解法
func diameterOfBinaryTree(root *TreeNode) int {
ans := 0
maxDepth(root, &ans)
return ans
}
// 由于树的直径并不一定会经过树的root,但是观察后可以发现
// 对于整棵树而言,diameter是以某个node为root,这个node的左树最大深度 + 右树最大深度
// 也就是我们计算出所有node为root的左树最大深度+右树最大深度,最后返回过程中的最大值即可
func maxDepth(root *TreeNode, d *int) int {
if root == nil {
return 0
}
ld := maxDepth(root.Left, d)
rd := maxDepth(root.Right, d)
// 由于递归计算,这里实际是bottom-up计算,不断更新d的值
*d = max(*d, ld+rd)
// 左右子树的最大相对深度 + 1 为当前root的相对深度
return max(ld, rd) + 1
}
func max(a int, b int) int {
if a >= b {
return a
}
return b
}