问题描述
You are given an array trees where trees[i] = [xi, yi] represents the location of a tree in the garden.
You are asked to fence the entire garden using the minimum length of rope as it is expensive. The garden is well fenced only if all the trees are enclosed.
Return the coordinates of trees that are exactly located on the fence perimeter.
Example 1:
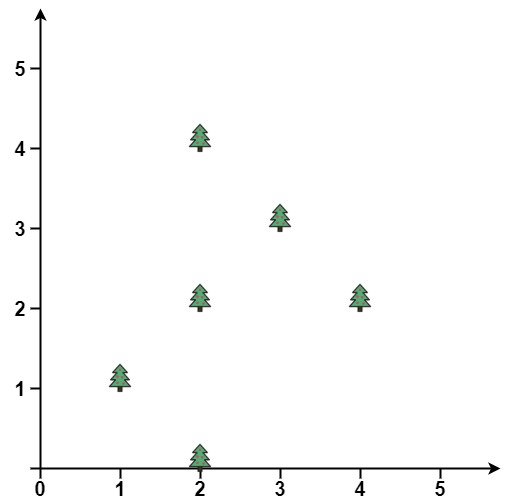
Input: points = [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2] ]
Output: [[1,1],[2,0],[3,3],[2,4],[4,2] ]
Example 2:

Input: points = [[1,2],[2,2],[4,2] ]
Output: [[4,2],[2,2],[1,2] ]
Constraints:
- 1 <= points.length <= 3000
- points[i].length == 2
- 0 <= xi, yi <= 100
- All the given points are unique.
问题分析
依据题意,我们需要用一根绳子将这些树都围起来,然后拉紧绳子,最后会得到一个多边形;求解哪些树是在这个多边形上(顶点或者边)
换言之,就是给定一些坐标点,求能够围住这些点的最小凸多边形
凸多变形: 凸多边形是一个内部为凸集的简单多边形。 凸多边形(Convex Polygon)指如果把一个多边形的所有边中,任意一条边向两方无限延长成为一直线时,其他各边都在此直线的同旁,那么这个多边形就叫做凸多边形,其内角应该全不是优角,任意两个顶点间的线段位于多边形的内部或边上。
凸多边形相关的算法属于知识盲区😭,只能求助于网络了。经过一番搜索,对于构建凸包,有一个相对简单的算法:Grahan Scan; 其算法复杂度为O(n logn)
Grahan Scan算法依赖这样一个几何知识:二维向量的叉积,或者也叫叉乘
二维向量的叉积: 向量a(x1, y1), b(x2, y2)
a x b = x1 * y2 - x2 * y1
几何意义为 |a| * |b| * sin<a, b>
如果 a与b的夹角小于180度(逆时针),这个值为正值;否则为负值
由于定义里有逆时针要求,所以 a x b 与 b x a 结果是不一样的
有了向量叉积的知识后,我们就能判断3个点构成的2个向量是向外“凸”还是向内“凹”的。基于这点,Grahan Scan算法主要分2大步骤:
- 对坐标点排序;x坐标小的靠前;如果x坐标相同,y坐标小的靠前
- 对排好序的点,分别构建上下2个“凸壳”; 构建完,进行合并,最终得到凸包
具体计算步骤见如下代码:
示例代码
// Graham Scan
/*
* 二维向量的叉积: 向量a(x1, y1), b(x2, y2)
* a x b = x1*y2 - x2*y1
* 几何意义为 |a| * |b| * sin<a, b>
* 如果 a与b的夹角小于180度(逆时针),这个值为正值;否则为负值
*/
func outerTrees(trees [][]int) [][]int {
if len(trees) <= 1 {
return trees
}
// 坐标排序
sort.Slice(trees, func(i, j int) bool {
if trees[i][0] == trees[j][0] {
return trees[i][1] < trees[j][1]
} else {
return trees[i][0] < trees[j][0]
}
})
// 构成凸包的点的下标集合
// base case: 最左侧的点必定在凸包中
ansidx := []int{0, 1}
// 1. 查找凸壳的下半部分
for i := 2; i < len(trees); i++ {
// 循环判断当前点i与已有的点是否维持凸包的“凸”性质
for len(ansidx) > 1 {
// 如果a,b向量叉积大于等于0,说明夹角小于等于180度,停止循环,将当前点加入ansidx
if det(trees[ansidx[len(ansidx)-1]], trees[ansidx[len(ansidx)-2]], trees[i]) >= 0 {
break
}
// 移除最后1个元素,继续判断
ansidx = ansidx[:len(ansidx)-1]
}
ansidx = append(ansidx, i)
}
// 2. 查找凸壳的上半部分
// 在查找下半部分凸壳时,最右侧的点一定已经在集合里了;所以这里倒序从倒数第2个元素开始,查找上半部分凸壳
for i := len(trees) - 2; i >= 0; i-- {
// 循环判断当前点i与已有的点是否维持凸包的“凸”性质
for len(ansidx) > 1 {
// 如果a,b向量叉积大于等于0,说明夹角小于等于180度,停止循环,将当前点加入ansidx
if det(trees[ansidx[len(ansidx)-1]], trees[ansidx[len(ansidx)-2]], trees[i]) >= 0 {
break
}
// 移除最后1个元素,继续判断
ansidx = ansidx[:len(ansidx)-1]
}
ansidx = append(ansidx, i)
}
ans := [][]int{}
// 部分or全部点在一条直线的情况下,会有重复,进行去重处理
m := make(map[int]int)
for _, v := range ansidx {
if _, ok := m[v]; !ok {
m[v] = v
ans = append(ans, trees[v])
}
}
return ans
}
// 根据3个点计算向量叉积
// mid中间点,left左侧点,right右侧点
func det(mid []int, left []int, right []int) int {
// 向量a
va := []int{right[0] - mid[0], right[1] - mid[1]}
// 向量b
vb := []int{left[0] - mid[0], left[1] - mid[1]}
// 叉积(逆时针)
return va[0]*vb[1] - va[1]*vb[0]
}