题目描述
Given strings s1, s2, and s3, find whether s3 is formed by an interleaving of s1 and s2.
An interleaving of two strings s and t is a configuration where they are divided into non-empty substrings such that:
- s = s1 + s2 + … + sn
- t = t1 + t2 + … + tm
- |n - m| <= 1
- The interleaving is s1 + t1 + s2 + t2 + s3 + t3 + … or t1 + s1 + t2 + s2 + t3 + s3 + … Note: a + b is the concatenation of strings a and b.
Example 1:
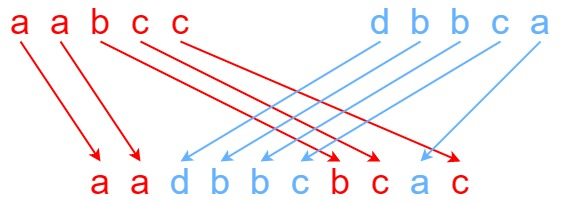
Input: s1 = “aabcc”, s2 = “dbbca”, s3 = “aadbbcbcac”
Output: true
Example 2:
Input: s1 = “aabcc”, s2 = “dbbca”, s3 = “aadbbbaccc”
Output: false
Example 3:
Input: s1 = “”, s2 = “”, s3 = ""
Output: true
Constraints:
- 0 <= s1.length, s2.length <= 100
- 0 <= s3.length <= 200
- s1, s2, and s3 consist of lowercase English letters.
Follow up: Could you solve it using only O(s2.length) additional memory space?
题目分析
初看题目,没有特别好的解法;试过用dp,但是状态转移方程没有想好应当怎么建议;
那么就先用“模拟”法尝试下,不妨假设s1的第一个字符和s3的第一个字符相同,那么第一步我们使用s1的第一个字符;在此基础上,我们记录s1和s2被分割的子串数量,以及上一次被分割的字符;那么按照如下规则继续进行:
- 如果s1的第二个字符和s3第二个字符相等,那么s1的段落数不变,继续下一轮判断
- 如果s2的第二个字符和s3第二个字符相对,那么s2段落数加1,上一次被分割的字符变为s2,继续下一轮判断
通过以上方式来模拟整个子串切割,最终判断组成s3后,s1和s2的分割子串数量差异是否在1之内
综上,代码如下:
初始解法
func isInterleave(s1 string, s2 string, s3 string) bool {
if len(s1)+len(s2) != len(s3) {
return false
}
return check(s1, s2, s3, 0, 0, 0) || check(s1, s2, s3, 0, 0, 1)
}
func check(s1 string, s2 string, s3 string, chunks1 int, chunks2 int, laststr int) bool {
ans := false
if abs(chunks1-chunks2) > 1 {
return ans
}
if len(s1) == 0 && len(s2) == 0 && len(s3) == 0 {
return true
}
if laststr == 0 {
if len(s1) > 0 && s1[0] == s3[0] {
ans = ans || check(s1[1:], s2, s3[1:], chunks1, chunks2, laststr)
if ans {
return ans
}
}
if len(s2) > 0 && s2[0] == s3[0] {
ans = ans || check(s1, s2[1:], s3[1:], chunks1, chunks2+1, laststr^1)
if ans {
return ans
}
}
}
if laststr != 0 {
if len(s1) > 0 && s1[0] == s3[0] {
ans = ans || check(s1[1:], s2, s3[1:], chunks1+1, chunks2, laststr^1)
if ans {
return ans
}
}
if len(s2) > 0 && s2[0] == s3[0] {
ans = ans || check(s1, s2[1:], s3[1:], chunks1, chunks2, laststr)
if ans {
return ans
}
}
}
return ans
}
func abs(a int) int {
if a < 0 {
return -1 * a
}
return a
}
优化代码
上述解法提交AC后,发现效率很低,已经是秒级了;
查看了评论区的优化解法,发现还是通过dp方式解决,优化解法中dp的定义为
dp[i][j] 表示 s1[:i], s2[:j], s3[:i+j]的解
这个初看不太好理解,我们可以将s1字符看做一个matrix的行,s2看做这个matrix的列,即:
s2 s2 s2 s2
s1 X - a - X - b - X - c - X
| | | |
a a a a
| | | |
s1 X - a - X - b - X - c - X
| | | |
c c c c
| | | |
s1 X - a - X - b - X - c - X
| | | |
d d d d
| | | |
s1 X - a - X - b - X - c - X
每一行边上的字符构成s1
每一列边上的字符构成s2
图中的X表示空,字符是在各个边上
那么原问题就变成了从左上角开始,只允许往右、往下移动
要走到右下角,是否存在一条这样的路径,使得经过的边上的字符构成s3
如果dp[i][j]表示上图中的点,那么到达这个点,只有2种方式,要么经过dp[i-1][j], 要么经过dp[i][j-1]
那么就有 dp[i][j] = (dp[i-1][j] && s1[i-1] == s3[i+j-1]) || (dp[i][j-1] && s2[i-1] == s3[i+j-1])
即dp[i-1][j]为真,且对应的字符也和s3中对应字符相等,否则就为false; 另一个方向也是如此;最终两者取或
所以综上,dp解法如下:
// dp
func isInterleaveV2(s1 string, s2 string, s3 string) bool {
if len(s1)+len(s2) != len(s3) {
return false
}
// dp[i][j] 表示字符串s1[:i], s2[:j], s3[i+j] 的解
dp := [][]bool{}
for i := 0; i <= len(s1); i++ {
dp = append(dp, make([]bool, len(s2)+1))
}
for i := 0; i <= len(s1); i++ {
for j := 0; j <= len(s2); j++ {
// base case
if i == 0 && j == 0 {
dp[i][j] = true
continue
}
// s1为空时,dp[i][j]取决于s2当前字符和s3当前字符是否相同
if i == 0 {
dp[i][j] = dp[i][j-1] && s2[j-1] == s3[i+j-1]
continue
}
// 同上, s2为空时,dp[i][j]取决于s1当前字符和s3当前字符是否相同
if j == 0 {
dp[i][j] = dp[i-1][j] && s1[i-1] == s3[i+j-1]
continue
}
// i, j都大于0时: dp[i][j]要么由dp[i-1][j]而来,要么由dp[i][j-1]而来,那么结果等于这两者的或
dp[i][j] = (dp[i-1][j] && s1[i-1] == s3[i+j-1]) || (dp[i][j-1] && s2[j-1] == s3[i+j-1])
}
}
return dp[len(s1)][len(s2)]
}
/* =========================================================================== */