题目描述
Nearly everyone has used the Multiplication Table. The multiplication table of size m x n is an integer matrix mat where mat[i][j] == i * j (1-indexed).
Given three integers m, n, and k, return the kth smallest element in the m x n multiplication table.
Example 1:
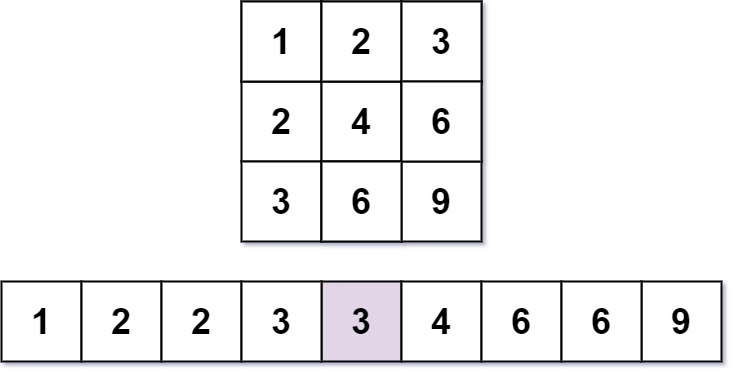
Input: m = 3, n = 3, k = 5
Output: 3
Explanation: The 5th smallest number is 3.
Example 2:
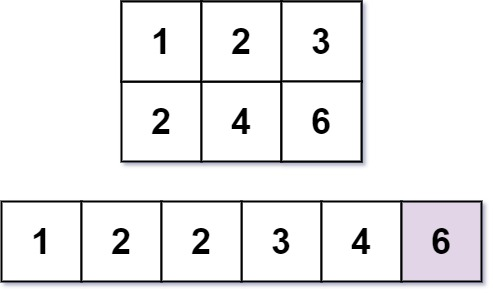
Input: m = 2, n = 3, k = 6
Output: 6
Explanation: The 6th smallest number is 6.
Constraints:
1 <= m, n <= 3 * 10^41 <= k <= m * n
题目分析
题目需要我们找到第k大的元素,如果m,n较小,可以考虑使用最大堆解决,那么整体复杂度为O(m * n * logk),整体来看复杂度还是太高
其次,我们可以看到对于整数N,如果可以分解为2个小于m、n的数的乘积,那么整数N必定存在于矩阵中;因此,我们可以让N从1不断递增,然后去找出N的因素分解的数量,直到总数量为k。这个算法的复杂度仍然太高,经过测试发现,对30000 * 30000的矩阵,短时间内已经无法得出结果。
对于有序矩阵而言,很明显,左上角元素最小,右下角元素最大。这个问题我们可以用二分搜索来解决。
-
首先,初始的
l,r分别为左上角元素1, 右下角元素m*n;cnt用来统计小于mid的元素数量 -
我们计算出中间数字
mid,然后对每一行,进行二分查找; -
对于某一行而言,如果mid比这一行的最后一个元素还要大,那么说明这一行都小于
mid,那么有cnt += n -
如果
mid比当前行最后一个元素要小,那么当前行中,小于mid的元素数量为mid / i,i为行号,下标从1开始 -
对所有行执行完一轮二分查找后,我们得出最终小于
mid的元素数量为cnt; 如果cnt小于目标值k,说明l需要增大; 如果cnt >= k,那么我们需要缩小r
按照上述方式,不断对矩阵所有行进行二分查找后,最终当 l == r终止循环时,有cnt == k,我们也就找到了第k大的元素
示例代码
func findKthNumber(m int, n int, k int) int {
// 左上角, 右下角
l, r := 1, m*n
for l < r {
mid := l + (r-l)/2
cnt := 0
// 逐行统计小于mid的元素数量
for i := 1; i <= m; i++ {
// 如果当前行最后1个数小于mid,则加上当前行数量
if n*i < mid {
cnt += n
} else {
// 否则第i行小于mid的数量为 mid / i
cnt += mid / i
}
}
// 如果当前统计的数量小于k,说明l需要增大
if cnt < k {
l = mid + 1
} else {
r = mid
}
}
return l
}
优化解法
Submission中速度靠前的解法和上述解法(32ms)差不多,但是仅需11ms。对比后发现,核心思想都是一致的,区别在于如何计算cnt
更高效的版本中,利用循环找到符合提交的最大的j,然后直接加到cnt中;猜测是这一步对cpu执行更为友好,不需要利用除法,因此执行速度更快
代码如下
func findKthNumber(m int, n int, k int) int {
// base case
if k == m*n {
return m * n
}
// k为1, 2 or 仅有1行或者1列
if k < 3 || m == 1 || n == 1 {
return k
}
l, r := 1, m*n
for l < r {
mid := l + (r-l)/2
cnt := 0
j := n
// 遍历每一行
for i := 1; i <= m; i++ {
// 对于每一行,从右下角开始,检查 i*j是否满足 i*j > mid
// 如果不满足,则停止循环; 此时,i*j <= mid
// 即当前第i行的前j个元素都小于等于 mid
for j > 0 && i*j > mid {
j--
}
// 加上j, 继续遍历下一行
cnt += j
}
if cnt < k {
l = mid + 1
} else {
r = mid
}
}
return l
}