题目描述
Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
Example 1:
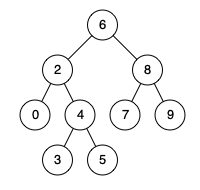
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.
Example 2:

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
Example 3:
Input: root = [2,1], p = 2, q = 1
Output: 2
Constraints:
- The number of nodes in the tree is in the range [2, 10^5].
- -10^9 <= Node.val <= 10^9
- All Node.val are unique.
- p != q
- p and q will exist in the BST.
题目分析
这道问题比较简单,由于是一棵BST,如果同时从root开始查找p,q的位置,那么当两者开始向某个节点的左右子树分别向下查找时,那么这个节点即为p,q的LCA。
综上,代码如下
实例代码
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
func lowestCommonAncestorV2(root, p, q *TreeNode) *TreeNode {
pv, qv := p.Val, q.Val
for root != nil {
// 如果都小于当前节点,则向左子树查找
if pv < root.Val && qv < root.Val {
root = root.Left
} else if pv > root.Val && qv > root.Val {
// 否则进入右子树
root = root.Right
} else {
// 如果此时开始分叉,则当前节点即为LCA
return root
}
}
return root
}