题目描述
You are given an m x n integer array grid where grid[i][j] could be:
- 1 representing the starting square. There is exactly one starting square.
- 2 representing the ending square. There is exactly one ending square.
- 0 representing empty squares we can walk over.
- -1 representing obstacles that we cannot walk over. Return the number of 4-directional walks from the starting square to the ending square, that walk over every non-obstacle square exactly once.
Example 1:
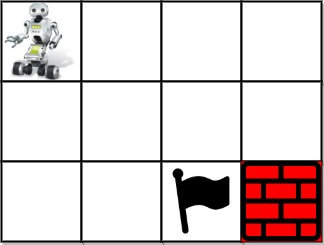
Input: grid = [[1,0,0,0],[0,0,0,0],[0,0,2,-1] ]
Output: 2
Explanation: We have the following two paths:
(0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2)
(0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2)
Example 2:
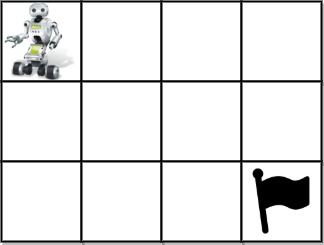
Input: grid = [[1,0,0,0],[0,0,0,0],[0,0,0,2] ]
Output: 4
Explanation: We have the following four paths:
- (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2),(2,3)
- (0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3),(1,3),(2,3)
- (0,0),(1,0),(2,0),(2,1),(2,2),(1,2),(1,1),(0,1),(0,2),(0,3),(1,3),(2,3)
- (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2),(2,3)
Example 3:

Input: grid = [[0,1],[2,0] ]
Output: 0 Explanation: There is no path that walks over every empty square exactly once. Note that the starting and ending square can be anywhere in the grid.
Constraints:
- m == grid.length
- n == grid[i].length
- 1 <= m, n <= 20
- 1 <= m * n <= 20
- -1 <= grid[i][j] <= 2
- There is exactly one starting cell and one ending cell.
题目分析
题目给定有且仅有1个起始点与结束点,其余格子则代表空(可以通行) 或者 障碍(不可通行)
按照通常dfs思路,我们需要从起始点开始,逐步探测,直至终点;但这次多了一些限制条件:
- 终点未知
- 到达终点时,所有空白格子都要走到
- 障碍格子不可通行
- 需要统计达到终点的路径总共有多少种
我们不妨倒过来,假设我们已经在终点,那么显然,到达终点的路径数量等于到达上下左右4个格子的路径数量之和;不妨以“上”格子为例,我们需要知道到达这个格子,且经过所有空白格子,但不含终点的路径数量;按照上述分析,我们已经可以得到动态规划问题的状态转移方程:
f((row, col)) = f((row-1, col)) + f((row, col-1)) + f((row+1, col)) + f((row, col+1))
当我们遍历到起始点时,只需判断经过的空白格子数量是否等于整个grid中空白格子数量;如果一致,说明我们找到了一条路径
综上,我们就可以从终点出发,递归求解,具体解法如下:
初步解法
var directions [][]int
func uniquePathsIII(grid [][]int) int {
// 初始化
directions = [][]int{
{-1, 0},
{1, 0},
{0, -1},
{0, 1},
}
rows := len(grid)
cols := len(grid[0])
// 障碍物数量
brickNum := 0
// 起始点、终点
start, end := point{}, point{}
// 1. 找到起止点, 统计障碍点数量
for row := 0; row < rows; row++ {
for col := 0; col < cols; col++ {
if grid[row][col] == -1 {
brickNum++
} else if grid[row][col] == 1 {
start.row = row
start.col = col
} else if grid[row][col] == 2 {
end.row = row
end.col = col
}
}
}
// 2. 到达结束点的路径数量为 以该点相邻点为结束点 且 穿过了所有0点的路径数量之和
// 递推而得,需要从结束点向开始点遍历,将相邻点依次作为结束点,递归查找
visited := make(map[int]bool)
return travel(grid, rows, cols, brickNum, start, end, visited)
}
type point struct {
row int
col int
}
func travel(grid [][]int, rows int, cols int, brickNum int, start point, end point, visited map[int]bool) int {
if grid[end.row][end.col] == -1 {
return 0
}
// 遍历到起始点
if grid[end.row][end.col] == 1 {
// 除起始点和障碍点外,都访问过
if len(visited) == rows*cols-1-brickNum {
return 1
}
// 还有未访问的0点
return 0
}
// 如果当前点已经访问过,直接返回0
if _, ok := visited[end.row*cols+end.col]; ok {
return 0
}
ans := 0
visited[end.row*cols+end.col] = true
for _, v := range directions {
newrow, newcol := end.row+v[0], end.col+v[1]
// 边界条件
if newrow < 0 || newrow >= rows || newcol < 0 || newcol >= cols {
continue
}
newend := point{
row: newrow,
col: newcol,
}
newvisited := make(map[int]bool)
for k, v := range visited {
newvisited[k] = v
}
// dfs 相邻点
ans += travel(grid, rows, cols, brickNum, start, newend, newvisited)
}
return ans
}
优化解法
上述解法AC后,整体效率一般,耗时60ms左右;查看排名靠前的解法,发现也是利用dfs,但是利用了回溯去解决普通dfs过程中需要反复构建visited map的过程,使得整体效率大为提升;
优化解法如下:
var directions [][]int
func uniquePathsIII(grid [][]int) int {
// 初始化
directions = [][]int{
{-1, 0},
{1, 0},
{0, -1},
{0, 1},
}
rows := len(grid)
cols := len(grid[0])
startRow, startCol := 0, 0
// 所有0的数量N,加上起始点;故初始值为1
// 这里不再统计障碍物数量,直接统计空白格子数量
zeros := 1
for row := 0; row < rows; row++ {
for col := 0; col < cols; col++ {
if grid[row][col] == 1 {
// start point
startRow = row
startCol = col
} else if grid[row][col] == 0 {
zeros++
}
}
}
return dfs(grid, startRow, startCol, rows, cols, zeros)
}
// 其中的cnt表示还剩余多少空白格子需要遍历
func dfs(grid [][]int, row int, col int, rows int, cols int, cnt int) int {
// 边界条件
if row < 0 || row >= rows || col < 0 || col >= cols || grid[row][col] == -1 {
return 0
}
// 遇到结束点
if grid[row][col] == 2 {
// 当前剩余待遍历点为0,说明已经全部遍历完,找到一条路径
if cnt == 0 {
return 1
}
return 0
}
// 当前已遍历点置为-1,进行标记
grid[row][col] = -1
ans := 0
for _, v := range directions {
newrow, newcol := row+v[0], col+v[1]
ans += dfs(grid, newrow, newcol, rows, cols, cnt-1)
}
// 回溯,将当前点再置为0
grid[row][col] = 0
return ans
}